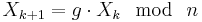Lehmer random number generator

The Lehmer random number generator[1] (named after D. H. Lehmer), sometimes also referred to as the Park–Miller random number generator (after Stephen K. Park and Keith W. Miller), is a variant of linear congruential generator (LCG) that operates in multiplicative group of integers modulo n. A general formula of a random number generator (RNG) of this type is:

X_{k%2B1} = g \cdot X_k~~\bmod~~n

where the modulus n is a prime number or a power of a prime number, the multiplier g is an element of high multiplicative order modulo n (e.g., a primitive root modulo n), and the seed X0 is co-prime to n.

Contents

Parameters in common use

In 1988, Park and Miller[2] suggested a Lehmer RNG with particular parameters n = 231 − 1 = 2,147,483,647 (a Mersenne prime M31) and g = 75 = 16,807 (a primitive root modulo M31), now known as MINSTD. Although MINSTD was later criticized by Marsaglia and Sullivan,[3] it is still in use today (in particular, in CarbonLib).

ZX Spectrum uses the Lehmer RNG with parameters n = 216 + 1 = 65,537 (a Fermat prime F4) and g = 75 (a primitive root modulo F4). The CRAY random number generator RANF is a Lehmer RNG with n = 248 and g = 44,485,709,377,909.[4] Another popular pair of parameters is n = 232 − 5 = 4,294,967,291 and g = 279,470,273.

LC53[5] in Forth (programming language) uses parameters n = 232 − 5 = 4,294,967,291 and g = 232 − 333333333 = 3,961,633,963.

The GNU Scientific Library includes several random number generators of the Lehmer form, including MINSTD, RANF, and the infamous IBM random number generator RANDU.[4]

Relation to LCG

While the Lehmer RNG can be viewed as a particular case of the linear congruential generator with c=0, it is a special case that implies certain restrictions and properties. In particular, for the Lehmer RNG, the initial seed X0 must be coprime to the modulus n that is not required for LCGs in general. The choice of the modulus n and the multiplier g is also more restrictive for the Lehmer RNG. In contrast to LCG, the maximum period of the Lehmer RNG equals n−1 and it is such when n is prime and g is a primitive root modulo n.

On the other hand, the discrete logarithms (to base g or any primitive root modulo n) of Xk in 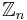\mathbb{Z}_n represent linear congruential sequence modulo Euler totient \phi(n).

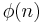Sample C99 code

Using C code, the Lehmer generator using the "popular pair" of parameters mentioned above can be written as follows:

uint32_t lcg_rand(uint32_t a)
{
    return ((uint64_t)a * 279470273UL) % 4294967291UL;
}

As the product of two 32 bit integers may overflow, the cast to uint64_t is necessary.

References

  1. ^ W.H. Payne, J.R. Rabung, T.P. Bogyo (1969). "Coding the Lehmer pseudo-random number generator". Communications of the ACM 12 (2): 85–86. doi:10.1145/362848.362860. http://www.firstpr.com.au/dsp/rand31/p85-payne.pdf. 
  2. ^ S. K. Park and K. W. Miller (1988). "Random Number Generators: Good Ones Are Hard To Find". Communications of the ACM 31 (10): 1192–1201. doi:10.1145/63039.63042. http://www.firstpr.com.au/dsp/rand31/p1192-park.pdf. 
  3. ^ Crawford, Diane (1993). "Technical correspondence". Communications of the ACM 36 (7): 105–110. doi:10.1145/159544.376068. 
  4. ^ a b GNU Scientific Library: Other random number generators
  5. ^ Novice Forth library